Integtrating Mathematics into Industries

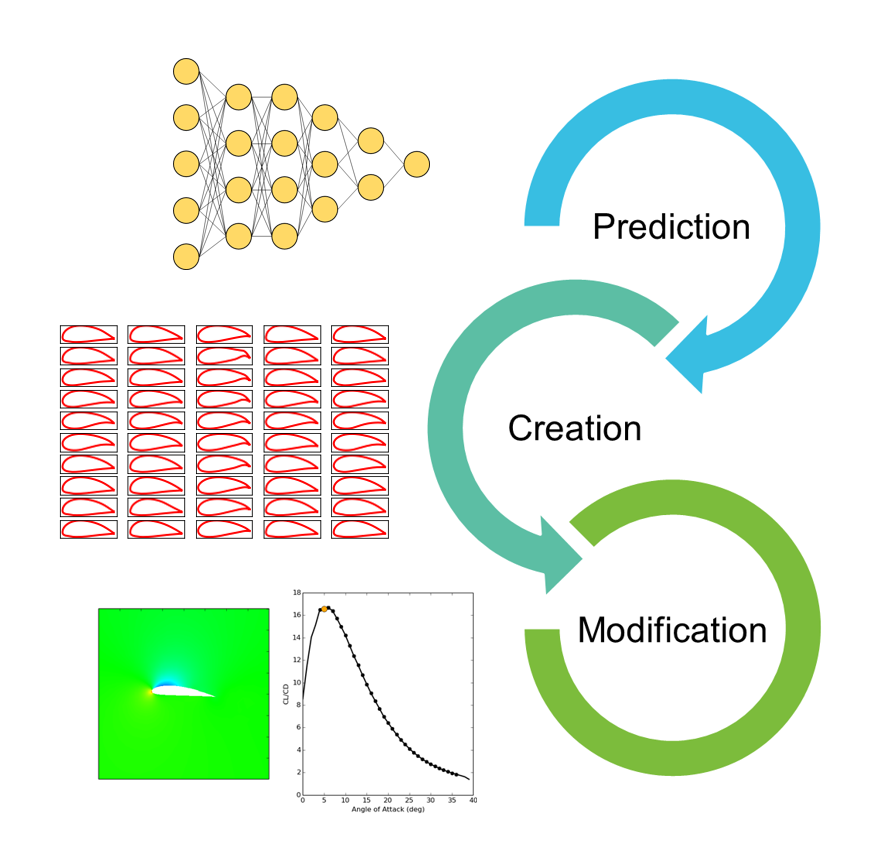
Data driven design

Our research is to design industrial products using machine learning and computational mechanics. Computational mechanics is used to compute mechanical properties o machines. By performing calculations on many types and shapes and analyzing the results using machine learning, we extract features that is common to good designs, and we find optimal shapes. Data driven design consists of three approaches; performance prediction, shape creation that finds a shape that meets specifications, and shape modification that slightly modifies the shape. Those aproaches utilize regression model, generative model, and reinforcement learning, respectively.

Mathematical Optimization and Design Optimization

Design optimization is to design an optimal shape that exhibits the best performance. Our research focuses on optimal design methods using mathematical optimization methods. For example, the framework called topology optimization has rich capability for changing the shape tht we can design products with higher performance. We have constructed a novel method of topology optimization that has reduced computation time to less than 1%.

Application of Machine Learning for Industries

This topic focuses on industrial application of machine learning. Although machine learning techniques have made great strides in recent years, there are still gaps in applying it to industrial fields. For example, there is a gap between social / industrial needs and technological seeds with respect to such as fail-safety and explanation capability. In addition, although there is a common standard for data inbalance, sometimes it may not work well when actually applied to a plant operation. Our research focuses to evelop the methodology to bridge the gap between such technological seeds and social / industrial needs; we are creating a mathematical method that meets the social / industrial needs, and developing a system configuration that matches the technological seeds to social needs.

Message

We solve social / industrial issues by using mathematics. Not only is mathematics itself attractive as a research object, it is also useful in solving social / industrial problems, and it is becoming more important as machine learning widespreads into society. We welcome those who are interested in integrating mathematical and social systems.